
안녕하세요. 훈릴스입니다.
오늘은 원뿔의 부피와 겉넓이를 구하는 방법에 대해 알아보는 시간을 가져보고자 합니다. 점점 입체도형이 까다로워지면서 외우는 공식들도 많아질 것으로 생각되네요. 단순 암기보다는 여러 문제풀이를 통해 익히면 더욱 머리에 잘 남을 것 같다는 생각이듭니다. 그럼 바로 알아봅시다 바로 레츠게릿!

원뿔의 부피를 구하는 방법은 위와 같습니다. 먼저 밑몉인 원의 넓이에 높이를 곱한 뒤 3으로 나누어주면 됩니다. 많은 분들이 왜 3으로 나누어지는지 궁금해하실 것으로 생각됩니다. 이것을 증명하려면 적분을 사용해야하는데요. 적분은 아직 중학교 과정에서 배우지 않는 수학 지식이기에, 단순히 적분을 이용해서 원뿔을 구했더니 위와 같은 공식이 나왔다고 알고 계시면 좋을 것 같습니다. 그렇다면 원뿔의 겉넓이를 구하는 공식은 어떻게 될까요? 바로 알아봅시다!

겉넓이 공식은 약간 복잡한데요. 우선 원뿔의 전개도를 펼쳐야합니다. 전개도를 펼치면 원 + 부채꼴이 나오죠. 겉넓이는 두개의 넓이의 합이됩니다. 원의 넓이는 위와 같습니다. 그 다음 부채꼴의 넓이를 구해야하는데요. 부채꼴의 넓이는 위의 그림에서 a곱하기 b에서 2를 나누어 주면 됩니다. 어려워보이지만 차근차근 따라오시면 간단하게 풀이하실 수 있을거에요!
그렇다면 이번에는 예시 문제를 한 번 풀어보겠습니다. 단순히 이론을 암기하는 것보다는 예시에 적응하면서 외우는 것이 더 잘 외워지고 머리에 오래남더라구요. 그럼 바로 문제를 제시하겠습니다.
문제. 다음과 같은 원뿔이 있을 때, 원뿔의 부피와 넓이를 구하여라.

어려워 보이지만 정보가 친절하게 잘 주어진 경우입니다. 차근차근 풀어봅시다. 먼저 부피부터 구해보도록 하겠습니다. 부피를 구하는 공식을 적용해서 풀면 다음과 같습니다.
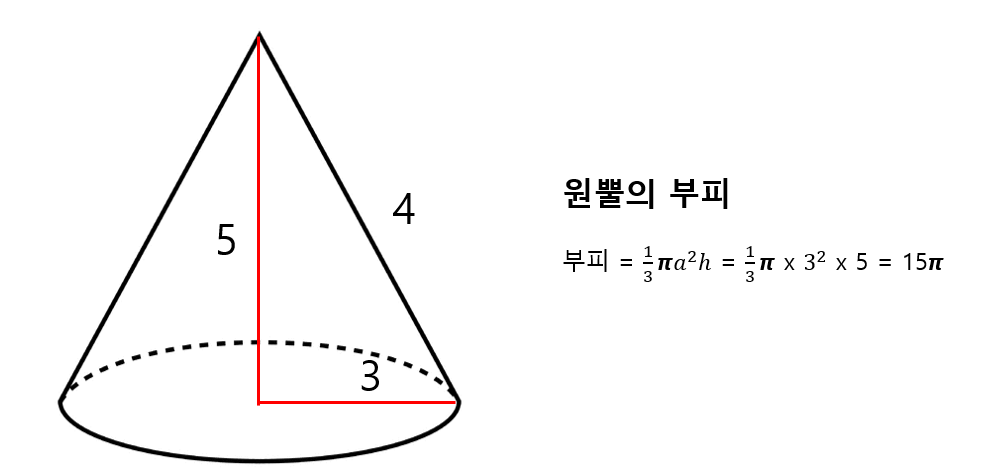
간단하게 밑면의 반지름의 넓이에 높이를 곱한 뒤, 3으로 나누어주면 됩니다! 간단하죠? 이제는 원뿔의 겉넓이를 구하는 방법을 알아봅시다. 풀이는 아래와 같습니다.
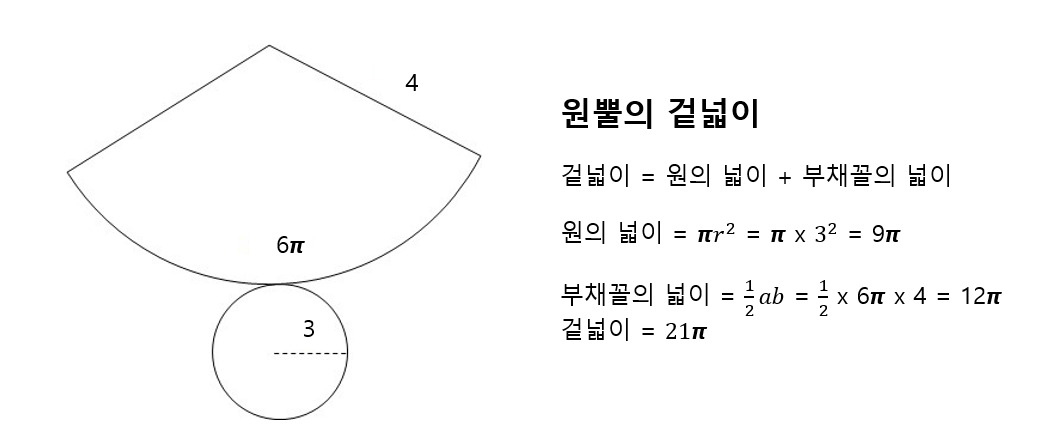
원뿔의 겉넓이를 구하는 방법은 다음과 같습니다. 우선 전개도를 펼쳐야하는데요. 전개도를 펼치면 각각의 길이는 위와 같습니다. 그 다음, 겉넓이는 원의넓이 + 부채꼴의 넓이이므로 각각의 넓이를 구한 뒤 더해주시면 됩니다.
조금은 복잡해보이지만 계속해서 문제를 풀다보고, 전개도를 열심히 그려보면 어느 순간 깨닫는 순간이 오실거에요. 수학이 쉬워지는 그날까지! 함께하겠습니다. 이상입니다.
'교육이야기' 카테고리의 다른 글
| 사각뿔 부피 겉넓이 구하기 법 (공식 총정리, 예제 풀이) (0) | 2022.03.24 |
|---|---|
| 원기둥 부피 겉넓이 구하는법 ( + 공식, 예제풀이) (0) | 2022.03.22 |
| 직육면체 부피 겉넓이 구하기(+예시 풀이 ) (0) | 2022.03.22 |
| 구의 부피 / 겉넓이 공식 정리 (+예시 풀이) (0) | 2022.03.22 |
| 원 직사각형 정사각형 사다리꼴 마름모 평행사변형 넓이 공식 정리 (0) | 2022.03.22 |




댓글