반응형

안녕하세요. 훈릴스입니다.
오늘은 삼각함수의 제곱공식을 정리해보는 시간을 가져보고자 합니다. 그럼 바로 레츠게릿
지난번 시간에 삼각함수를 정의할 때, 반지름이 1인 원을 이용해서 정의했지요. 지난번 시간 삼각함수의 정리는 다음과 같습니다.

여기서 sin의 제곱과 cos제곱을 더해볼게요. 무엇이 나오나요? 바로 원의 반지름인 r이나오겠지요. 앞서서 원의 반지름은 1이라고 정의했으니깐 우리는 여기서 제곱법칙을 발견할 수 있어요.

위의 제곱 법칙이 바로 가장 기본적인 삼각함수의 제곱 법칙입니다. 우리는 여기서 양변을 cos의 제곱으로 나눌 수 있는데요. cos으로 나누면 다음과 같이 변해요.
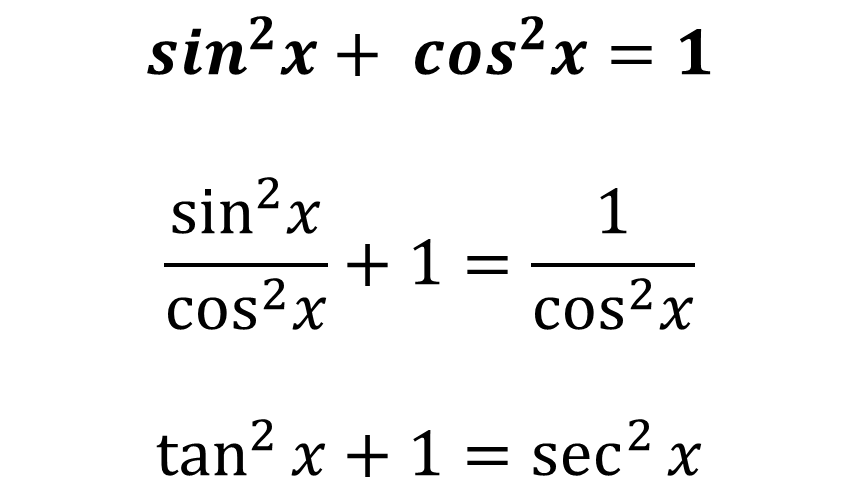
위의 변환을 통해서 삼각함수를 간단하게 만들거나 다른 식으로 변환할 수 있는 것이지요. 또한 양 변을 sin 제곱으로도 나눌 수 있는데요. 나누면 다음과 같이 변화한답니다.
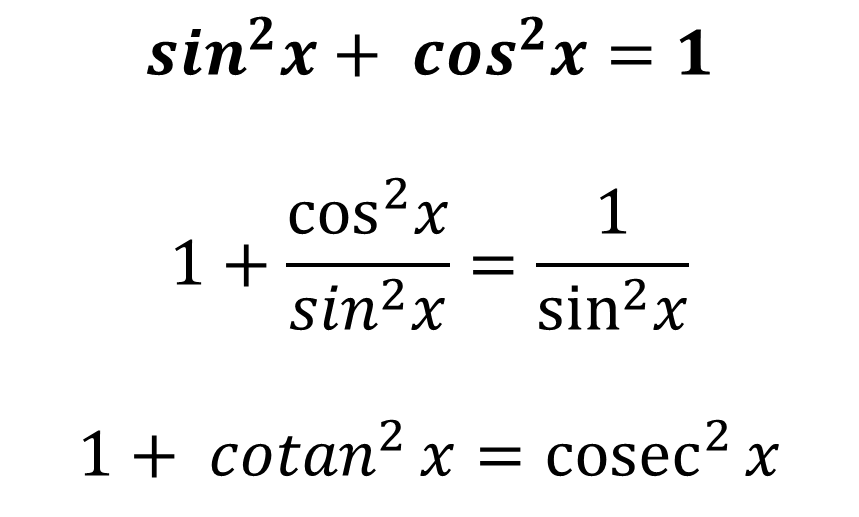
간단한 공식에서 양변을 sin이나 cos 등으로 나누어서 다양하게 표현할 수 있는 것이 삼각함수의 묘미인 것 같습니다. 처음에는 어려울지도 모르지만 찬찬히 익혀나가시면 나중에는 몸에 체화되셔서 편하게 사용하실 수 있으실 거에요! 기초가 정말 중요한 삼각함수입니다. 여러분께 도움이 되기 위해 많이 노력할게요!!
반응형
'교육이야기' 카테고리의 다른 글
| 삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이) (0) | 2022.03.24 |
|---|---|
| 사인법칙 총정리(공식, 예제 풀이) (0) | 2022.03.24 |
| 삼각함수 기본정리(얼싸탄코, sin, cos, tan) (0) | 2022.03.24 |
| 호도법은 무엇인가?( 호의길이 구하는법, 호의길이 공식, 부채꼴 면적) (0) | 2022.03.24 |
| 사각뿔 부피 겉넓이 구하기 법 (공식 총정리, 예제 풀이) (0) | 2022.03.24 |




댓글