반응형

안녕하세요. 훈릴스입니다.
오늘은 삼각함수 사인법칙에 대해 알아보는 시간을 가져보고자 합니다. 간단한 법칙이지만 간단한 여러 개념이 묶여서 여려운 문제가 출제되는 삼각함수 특성상 잘 알아두셔야할 것 같습니다. 그럼 바로 레츠게릿!
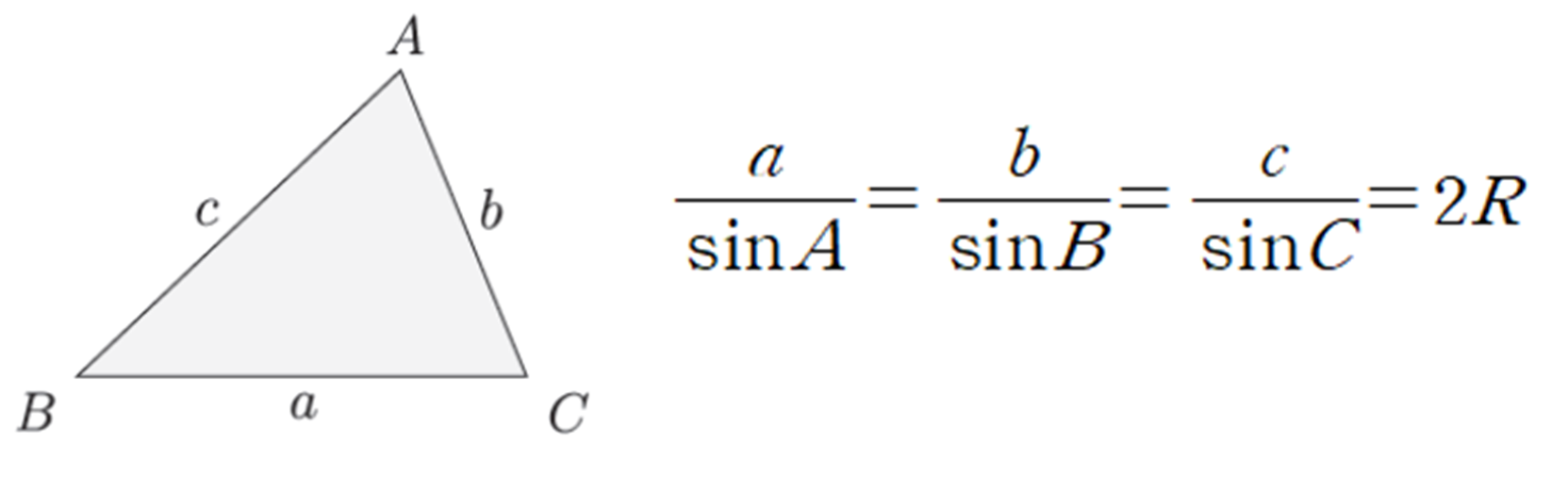
사인 법칙은 다음과 같습니다. 외우실 때, 각 A와 변 a의 비는 각 B와 변 b의 비와 같다는 것이죠. 그리고 이러한 비율은 2R과 동일한데, 여기서 R은 외접원의 반지름입니다. 이러한 공식을 이용해서 문제마다 주어진 조건을 이용하여 각이나 변의 길이를 구할 수 있는 것이죠. 같이 문제를 하나 풀어보면서 정리해봅시다!
문제) 다음과 같은 삼각형이 주어졌을 때 변AB의 길이는 얼마인가?

각 B와 각 C가 주어지고, 선분 AC의 길이가 5로 주어졌네요. 그냥 푼다면 어렵겠지만, 앞서 배운 사인법칙을 이용하면 간단하게 풀 수 있습니다. 앞서 배운 공식을 적용하면 다음과 같습니다.
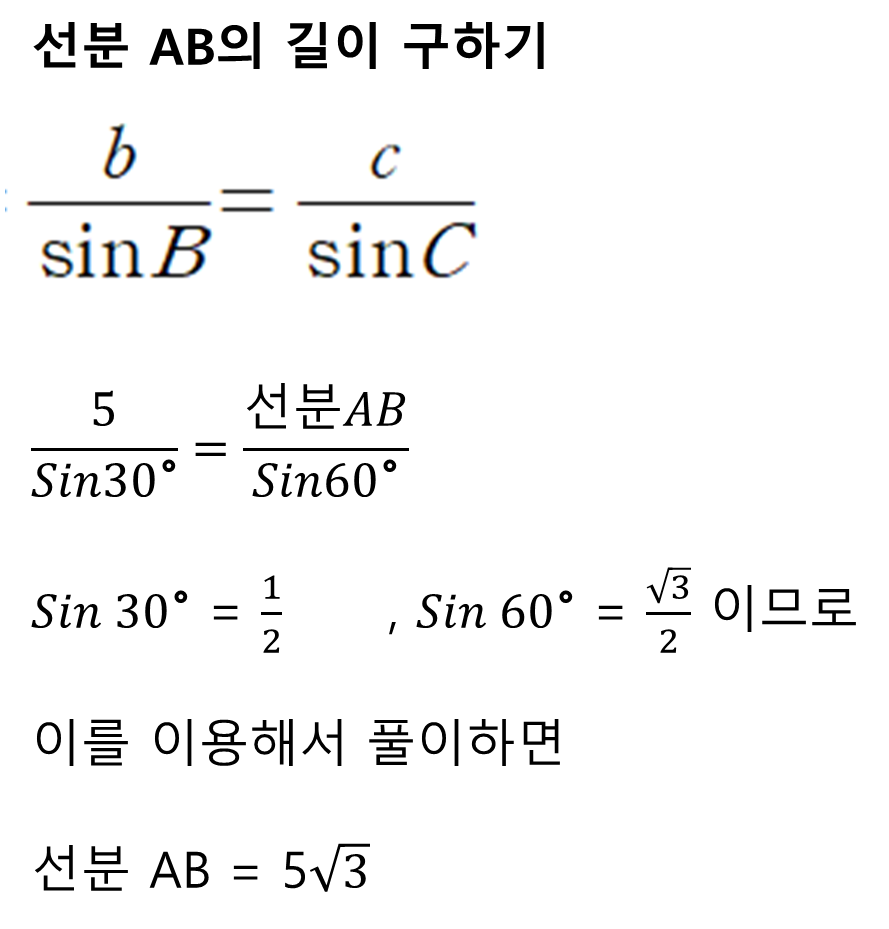
어려워 보이지만, 사인법칙을 이용하니 간단한 곱셈문제로 변했네요! 사인 법칙을 잘 알아두셔서 문제푸는데 유용하게 적용하시기를 바라요! 감사합니다.
반응형
'교육이야기' 카테고리의 다른 글
| 삼각함수의 덧셈법칙 공식 총정리(sin, cos, tan) (0) | 2022.03.24 |
|---|---|
| 삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이) (0) | 2022.03.24 |
| 삼각함수 제곱공식 정리(sin^2x+cos^2x=1) (0) | 2022.03.24 |
| 삼각함수 기본정리(얼싸탄코, sin, cos, tan) (0) | 2022.03.24 |
| 호도법은 무엇인가?( 호의길이 구하는법, 호의길이 공식, 부채꼴 면적) (0) | 2022.03.24 |




댓글