반응형

안녕하세요. 훈릴스입니다.
오늘은 삼각함수의 공식 중 제 2 코사인 법칙에 대해 알아보는 시간을 가져보고자 합니다. 요즘들어 삼각함수와 관련된 포스팅을 많이하고 있는데요. 정말 해도해도 끝이없는 것이 수험생 여러분들의 고통이 느껴집니다. 간단하니, 따라오시죠! 레츠게릿
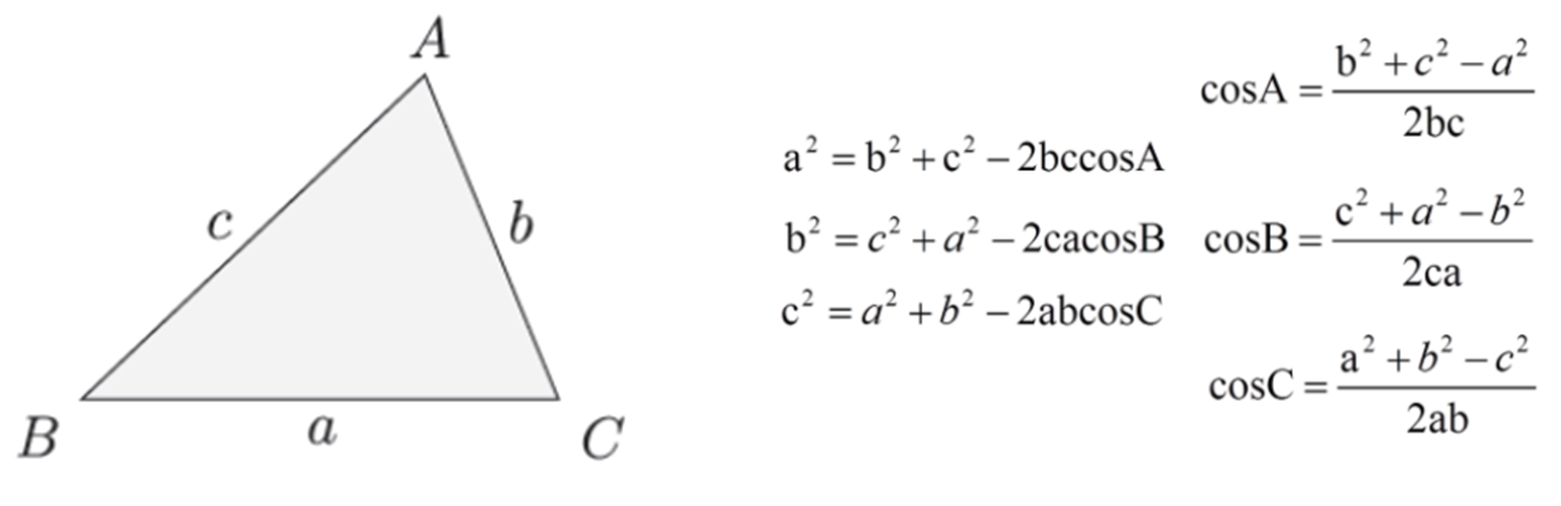
코사인 제 2법칙은 다음과 같습니다. 어려워보이지만 사실은 간단한데요. 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2를 곱하고 구하고자하는 변의 마주편 각의 Cos을 곱한 것과 같습니다. 말로 표현하자니 어렵지만, 열 번 정도 공책에 적어보시면 원리를 쉽게 익히실 수 있을 것입니다. 코사인 제 2법칙은 다양한 문제에 적용되기에 꼭 알고 계셔야하는데요. 공식만 알고가면 그러니, 바로 예제 문제 풀이를 해보겠습니다. 따라오시죠!
문제) 다음과 같은 삼각형이 주어졌을 때 c의 길이는 얼마인가?

문제가 주어졌네요. 각 하나와 변의 길이가 두 개가 주어지면 코사인 2법칙을 이용해서 풀어야한다고 머릿속에서 생각하셔야 해요. 앞서 배운 공식을 적용해서 문제 풀이를 진행하면, 다음과 같습니다.

간단하죠? 코사인 2법칙을 이용하는 문제를 자주 풀어보시면 자유자재로 문제 풀이가 가능하실 거에요! 오늘도 화이팅!!
반응형
'교육이야기' 카테고리의 다른 글
| 삼각함수의 합성법칙(공식, 예제풀이) (0) | 2022.03.24 |
|---|---|
| 삼각함수의 덧셈법칙 공식 총정리(sin, cos, tan) (0) | 2022.03.24 |
| 사인법칙 총정리(공식, 예제 풀이) (0) | 2022.03.24 |
| 삼각함수 제곱공식 정리(sin^2x+cos^2x=1) (0) | 2022.03.24 |
| 삼각함수 기본정리(얼싸탄코, sin, cos, tan) (0) | 2022.03.24 |




댓글