반응형

안녕하세요. 훈릴스입니다.
오늘은 삼각함수의 합성법칙을 이용해보는 시간을 가져보고자 합니다. 사실 다른 삼각함수의 법칙들에 비해서 사용량이 적은 공식입니다. 하지만, 대학교로 진학하시는 분이라면 꼭 알고계셔야해요. 실제로 공식을 유도할 때 많이 사용되는 법칙이거든요. 그러면 바로 레츠게릿!!
삼각함수의 덧셈법칙은 아래와 같습니다.
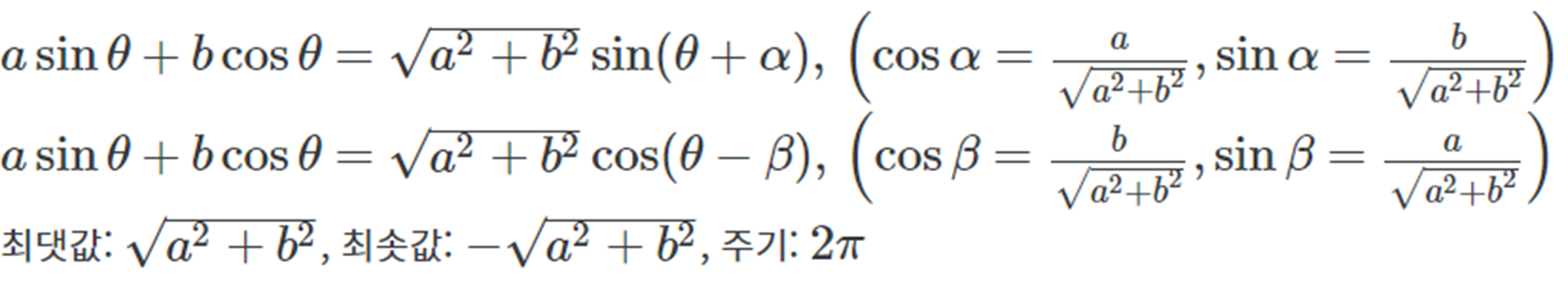
계수가 있는 sin과 cos을 하나의 삼각함수로 표현하는 방법인데요. 이것을 통해서 우리가 궁극적으로 알고자하는 것은 바로 최댓값과 최솟값을 구할 수 있다는 것입니다. 두 개의 항으로 표현하면 최댓값과 최솟값을 구하는 것이 쉽지 않기에 하나의 항으로 표현하는 것이죠. 그래서 합성함수는 공식을 유도하거나, 유도한 공식의 최댓값과 최솟값을 구할 때 많이 사용합니다.
이제 이러한 공식을 사용해서 최댓값과 최솟값을 구해보겠습니다. 단순히 공식을 아는 것과 적용해보는 것은 천지차이니깐요. 그럼 바로 문제를 풀어봅시다.
문제) 3sinX + 4cosX의 최댓값과 최솟값을 구하여라.
풀이 ) 두 개의 항이 있는 다항식의 최댓값과 최솟값을 구해야 하는군요. 간단합니다. 앞서 배운 공식을 바로 이용해보겠습니다.
3sinX + 4cosX = 5sin(X+a) --> sin(X+a)의 최댓값 : 1, 최솟값 : -1
그러므로 두 다항식의 최댓값은 5이고 최솟값은 -5입니다. 이렇게 두개의 항이 있는 식의 최댓값과 최솟값을 구할 수 있는 것이 바로 삼각함수의 합성입니다!! 감사합니다!
반응형
'교육이야기' 카테고리의 다른 글
| 삼각함수 공식 총 정리!!(덧셈법칙, 제곱공식, 사인법칙, 제2코사인법칙, 덧셈법칙, 2배각법칙, 합성법칙 등 공식모음) (0) | 2022.03.24 |
|---|---|
| 삼각함수 2배각 공식(sin2X, Cos2X, 문제풀이) (0) | 2022.03.24 |
| 삼각함수의 덧셈법칙 공식 총정리(sin, cos, tan) (0) | 2022.03.24 |
| 삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이) (0) | 2022.03.24 |
| 사인법칙 총정리(공식, 예제 풀이) (0) | 2022.03.24 |




댓글