
안녕하세요. 훈릴스입니다.
오늘은 삼각함수의 공식을 모두 한 번 정리해보는 시간을 가져보고자 합니다. 정말 기본중에 기본적인 공식들이니 꼭꼭 암기하셔야하는데요. 너무 급하게 외우시기 보다는 하루에 한 번씩 써보는 것도 좋은 공부법이라고 생각되네요.
1. 삼각함수란 무엇인가

삼각함수 sin, cos, tan는 반지름 길이가 1인 원을 가지고 정의를 하는데요. 원 위의 한 점을 P(x,y)라고 하면 위와 같이 sin, cos, tan를 나타낼 수 있는 것이죠. 이렇게 어려운 것을 왜 정의하느냐라고 의문을 가지고 계신 분들이 있으실 것으로 생각 되네요. 하지만, 기초 중에 기초인 삼각함수를 이용하면 "복잡한 식을 간단하게" 만들 수 있기 때문에 이용해요! 처음에는 외울 것도 많으니 어려움을 겪으시겠지만 하나하나 살펴보면 쉽게 이해할 수 있을 것 같아요.
2. 얼싸탄코는 무엇인가?
갑자기 무슨 말이냐라고 의문을 가지고 계신 분들이 계실 것으로 생각되네요! 위의 그림에서 삼각형의 각도에 따라서 삼각함수의 부호가 바뀌게 되는데요. 1사분면(0~90도)일 때는 sin,cos,tan 모두 양수죠! 2사분면(90~180도) 일때는 sin함수만 양수이고 cos과 tan는 음수에요. 3사분면(180~270도)에서는 tan만 양수이고, sin, cos는 음수에요. 4사분면(270~360도)에서는 cos만 양수이고 sin과 tan는 음수에요. 이렇게 각 사분면마다 양수인 부분만 따서 이름을 정한 것이 "얼싸탄코"라고 합니다!!
1사분면 - 얼(all) 모두 양수
2사분면 - 싸(sin) 만 양수
3사분면 - 탄(tan)만 양수
4사분면 - 코(cos)만 양수
이렇게 해서 "얼싸탄코"가 탄생하게 됐어요!!
3. 삼각함수 제곱공식은 무엇인가요?

sin의 제곱과 cos의 제곱을 더하면 1이나오는데, 이것을 제곱공식이라고 한답니다. 이러한 공식은 양변을 sin 제곱으로 나누거나 cos제곱으로 나누어서 다양한 형태로 표현이 가능한데요. 다음과 같습니다!


이렇게 다양하게 표현 가능한 것이 삼각함수의 제곱 공식이랍니다.
4. 사인법칙은 무엇인가요?

사인 법칙은 다음과 같습니다. 외우실 때, 각 A와 변 a의 비는 각 B와 변 b의 비와 같다는 것을 이용하면 쉽게 외우실 수 있을 것이에요. 그리고 이러한 비율은 2R과 동일한데, 여기서 R은 외접원의 반지름을 의미합니다. 이러한 공식을 이용해서 문제마다 주어진 조건을 이용하여, 각이나 변의 길이를 구할 수 있는 것입니다!!
5. 코사인 제2법칙은 무엇인가요?
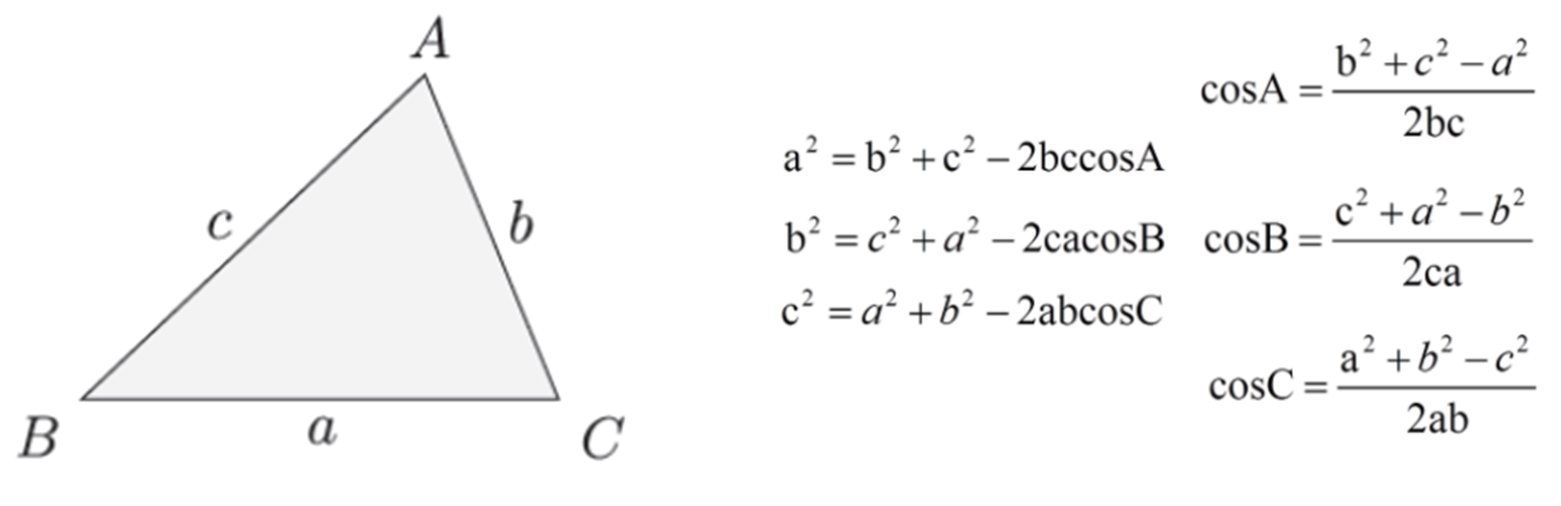
코사인 제 2법칙은 다음과 같아요. 어려워보이지만 사실은 간단해요!! 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2를 곱하고 구하고자하는 변의 마주편 각의 Cos을 곱한 것과 같답니다! 말로 표현하자니 어렵지만, 열 번 정도 공책에 적어보시면 원리를 쉽게 익히실 수 있을 것 같아요!. 코사인 제 2법칙은 다양한 문제에 적용되기에 꼭 알고 계셔야합니다!!
6. 삼각함수 덧셈법칙은 무엇인가요?
Sin(A+B) = SinA*CosB + CosA*SinB - 신코코신
Sin(A-B) = SinA*CosB - CosA*SinB
Cos(A+B) = CosA*CosB - SinA*SinB - 코코신신
Cos(A-B) = CosA*CosB + SinA*SinB

각의 합을 다양하게 덧셈으로 표현할 수 있는 것이 덧셈법칙의 묘미랍니다!!
7. 삼각함수의 합성법칙은 무엇인가요?

계수가 있는 sin과 cos을 하나의 삼각함수로 표현하는 방법입니다. 이것을 통해서 우리가 궁극적으로 알고자하는 것은 바로 최댓값과 최솟값을 구할 수 있다는 것이죠!! 두 개의 항으로 표현하면 최댓값과 최솟값을 구하는 것이 쉽지 않기에 하나의 항으로 표현하는 것입니다. 그래서 합성함수는 공식을 유도하거나, 유도한 공식의 최댓값과 최솟값을 구할 때 많이 사용합답니다!!
8. 삼각함수의 2배각 공식은 무엇인가요?

sin의 덧셈법칙을 이용해서 sin2X = 2sinXcosX 인 것을 증명할 수 있습니다. 마찬가지로 cos과 tan의 2배각 공식도 각각의 덧셈 법칙을 이용해서 증명할 수 있답니다. 증명하는 것은 여러분이 꼭 노트에 적으면서 한 번씩 해보시길 권해요. 어떻게 공식이 형성되는지 알 수 있다면 더 기억에 오래남을거에요!!
이상으로 삼각함수의 모든 공식에 대해 정리해보았습니다! 많아보이지만 하나하나 익히시면 서로 연결되어 있다는 것을 깨달으실 수 있으실 거에요!! 모두들 화이팅!!
'교육이야기' 카테고리의 다른 글
| 대기권에 대한 모든 것(대류권, 성층권, 중간권, 열권 총정리) (0) | 2022.03.26 |
|---|---|
| 무고죄란 무엇인가? (무고죄의 모든 것) (0) | 2022.03.25 |
| 삼각함수 2배각 공식(sin2X, Cos2X, 문제풀이) (0) | 2022.03.24 |
| 삼각함수의 합성법칙(공식, 예제풀이) (0) | 2022.03.24 |
| 삼각함수의 덧셈법칙 공식 총정리(sin, cos, tan) (0) | 2022.03.24 |




댓글